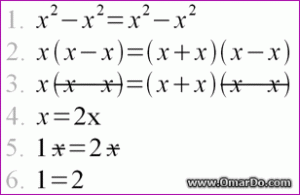Today was a big day. I moved into my room at University. I don't really feel ready for it. I don't think I've ever cried so much when my mum and my boyfriend left.
But my room is really nice. It is a decent size, and has everything I need in it to help me survive my first year at Uni.
I am going to miss everyone so much, but I still want to have a good time. Right now I still feel a bit helpless, but it should get better. I have an introductory lecture tomorrow morning, so that should clear some things up for me about my course, and I get to meet my personal tutor.
Can you tell I'm a maths student?
This is the start of a very big adventure.
Sunday, 30 September 2012
Tuesday, 25 September 2012
Fibonacci
Leonardo da Pisa (otherwise known as Fibonacci) was an Italian mathematician born around 1770. Fibonacci is known for popularising the Arabic numerals (1, 2, 3 etc.) in Christian Europe, but is probably most famous for the number sequence he published in his book, Liber Abaci. The Fibonacci Sequence. This sequence of numbers was actually already known to Indian mathematicians as early as the 6th Century, but Fibonacci was the one who introduced it to the West.
Fibonacci originally came across the sequence when trying to solve a problem to do with the growth rate of rabbit populations. His problem was this:
Let a pair of baby rabbits into a fenced off garden. After a month they will mature into adult rabbits. Every month after that they will produce another pair of rabbits. If every pair of rabbits follows this model, and assuming none of the rabbits die, how many rabbits will there be after a year?
Obviously this theoretical model was created based on some very crude assumptions. For starters, the rabbits never die (which clearly wouldn't happen). Also it assumes that rabbits mate for life, they consistently produce another pair every month who also mate for life, and only take a month to mature into rabbits who can reproduce. These assumptions meant that he wasn't accurately predicting the growth rates of rabbits, but he did produce a sequence that is still used today, in science and in nature!
This image shows how the model plays out when you apply the limitations and run it through. The orange rabbits are the babies, and the white rabbits are when they have matured. When an arrow points from a white pair to a white pair, it shows the same pair of rabbits. The sequence Fibonacci ended up with was 1, 1, 2, 3, 5, 8, 13, 21... and so on. This is the famous Fibonacci Sequence. It is so famous because it has some interesting properties.
- The most obvious property is that every term in the sequence is the sum of the previous two. For example, 1+1=2, 1+2=3, 2+3=5 and so on.
- When you add the terms of the sequence (1+1=2, 1+1+2=4, 1+1+2+3=7) the answers create a new sequence that is similar to the original. When you add n terms of the Fibonacci Sequence together, the total equals the (n+2)th (for want of a better description...) term minus 1. For example, if you add the first 5 terms of the Fibonacci Sequence, the answer is the 7th term of the Fibonacci Sequence minus 1.
New 2 4 7 12 20 33 54...
- When you add the squares of the Fibonacci numbers, you get another sequence. It just so happens there is an easy way to work out the sum up to the nth term of the squared sequence by using the Fibonacci Sequence. Say you want to work out the 5th term of the sum of squares, you take the 5th and 6th Fibonacci numbers and multiply them together. It comes out to the same number. In this case, 5x8=40.
Squares 1 1 4 9 25 64 169 441 1156 3025...
When you find the ratio between successive Fibonacci numbers, the ratios soon approach the number known as the Golden Ratio. The Golden Ratio is an irrational number (meaning the decimals don't end, and don't repeat in a pattern) that equals 1.618 to 3dp. The Golden Ratio (depicted by the Greek letter phi φ) can be shown as a rectangle, where the ratio of a:b is the same as the ratio of a+b:a (referring to the sides in the picture below).
When you draw the Fibonacci numbers as squares with side lengths corresponding to the number in the sequence, you end up with a picture like this.
Ignore the random line, I didn't count it correctly... Anyway, presenting the Fibonacci numbers in this way shows that it is a good approximation for the Golden Rectangle. The Golden Rectangle was thought to be the most pleasing rectangle by ancient scholars, and is used by many artists and architects. For example, the Parthenon in Athens, Greece, follows the Golden Rectangle, as does Leonardo da Vinci's Mona Lisa.
If you join the corners of the Golden Rectangle with a curved line, you end up with a spiral, known as (surprise, surprise) the Golden Spiral. The Fibonacci spiral is also a good approximation to this.
The Golden Spiral is found everywhere in nature. For example, the patterns on many different shells, such as snail shells, follows the same spiral. And of course, the picture that started off all of this research of mine:
That's it from me on Fibonacci. I've been trying to write this blog post for so long now, I think it's about time I actually finished it off and posted it.
Monday, 24 September 2012
Monday Maths Madness 10
This is one I see all over the place, especially on Facebook. It's pretty self explanatory I think. Simple and funny.
Four pictures today, you lucky things! This one a friend sent to me. I didn't actually know that one Newton per square metre is a Pascal, but I think you get the jist of the joke anyway (well, I did). It made me giggle, so I thought I'd share it.
Well that's it for this week. Enjoy :)
Monday, 17 September 2012
Monday Maths Madness 9
I don't have any pictures this week, so I thought I would share some interesting (well I think so anyway!) facts about a number everyone knows: 666.
The number 666 is probably most commonly known as the Number of the Beast, from the biblical book of Revelation. However, it also has some interesting mathematical properties. First of all, 666 is equal to the sum of the squares of the first seven primes (seven being considered a magic number, as an extra little fact). In other words:
As well as this cool coincidence, 666 is the sum of palindromic (meaning it reads the same backwards as it does forwards) cubes.
And just to add to the weirdness, the 63 in the centre is shorthand for 6 x 6 x 6.
So, is 666 the Number of the Beast, or the Number of the Numerologist?
The number 666 is probably most commonly known as the Number of the Beast, from the biblical book of Revelation. However, it also has some interesting mathematical properties. First of all, 666 is equal to the sum of the squares of the first seven primes (seven being considered a magic number, as an extra little fact). In other words:
666 = 22 + 32 + 52 + 72
+ 112 + 132 + 172
As well as this cool coincidence, 666 is the sum of palindromic (meaning it reads the same backwards as it does forwards) cubes.
666 = 13 + 23 + 33 + 43
+ 53 + 63 + 53 + 43 + 33
+ 23 + 13
And just to add to the weirdness, the 63 in the centre is shorthand for 6 x 6 x 6.
So, is 666 the Number of the Beast, or the Number of the Numerologist?
Monday, 10 September 2012
When my little brother sees my maths work
In preparation for University maths, I have been looking at some sample questions before I try an online test. I left it alone for a few minutes with my little brother and came back to this...
Clearly he wasn't a fan. Funnily enough, I was having trouble with the question, and was feeling a little 'sad face' myself. At least he didn't eat it, like he used to do with my homework.
Monday Maths Madness 8
More reality broken down into equations. I particularly like the modern art one. I sometimes really don't understand art. I'm still not convinced by the purple square I saw in the Tate gallery once.
The pigeons in this picture just happen to be sitting distances apart that reflect the distances between the numbers in the Fibonacci sequence (I still need to write that post. Soon I promise!) Even pigeons can do maths! Either that or it is a coincidence. Either way, it's pretty cool. I think so anyway.
I have no idea where this road is, but the caption on 9gag said that the road is a circle. As you know, pi is a ratio linked with circles, so that just makes this sign that much more awesome. I'm easily impressed aren't I?
Monday, 3 September 2012
Monday Maths Madness 7
I have more pictures!! Enjoy :)
Is it pi, or is it cake? Personally, I think it is a pake, just to confuse everyone more :) My sister made me a pake once. It was good.
I love 9gag. You can find some random things on there. Like this PIcycle. My step-dad might want one of these, although it does look like it might be kind of uncomfortable...
Poor little maths nerd. He made me laugh though.
Is it pi, or is it cake? Personally, I think it is a pake, just to confuse everyone more :) My sister made me a pake once. It was good.
I love 9gag. You can find some random things on there. Like this PIcycle. My step-dad might want one of these, although it does look like it might be kind of uncomfortable...
Poor little maths nerd. He made me laugh though.
Subscribe to:
Comments (Atom)